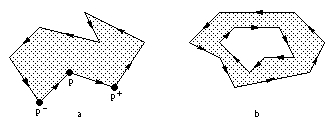
Fig. 1.1 -- Définition des polygones. a. Orientation des sommets. b. Polygone avec trou.
Si nous cherchons plutôt à visualiser une scène, seuls les objets visibles doivent apparaître à l'écran : il vaut mieux alors éviter de faire des calculs coûteux sur les objets cachés car le temps passé dans ces calculs n'aura pas d'incidences sur l'affichage de la scène.
Nous retrouvons aussi des problèmes de visibilité aussi au coeur des problèmes de surveillance ou d'éclairage.
Une grande partie des problèmes de planification de trajectoire concerne divers véhicules qui se déplacent au sol, c'est-à-dire sur un plan. Bien que l'image de synthèse concerne principalement des scènes dans l'espace 3D, certains problèmes de visualisation ont une base 2D : les calculs effectués pour afficher ce que voit un piéton se déplaçant dans une ville font intervenir le plan (2D) de la ville. Les problèmes de surveillance sont eux-aussi principalement des problèmes 2D. L'étude des relations de visibilité dans le plan n'est donc pas limitée à un seul intérêt théorique.
Les relations de visibilité dans le plan ont d'abord été étudiées sur des objets simples, notamment sur des ensembles de segments disjoints. Certains algorithmes ont même été adaptés à partir d'algorithmes opérant sur des ensembles de points (calcul de graphe de visibilité d'Edelsbrunner et Guibas [EG86] Le cas de scènes polygonales a été aussi abordé, mais beaucoup d'algorithmes ne considèrent en fait que des scènes composées d'un seul polygone, où l'espace libre de la scène est limité à l'intérieur du polygone (calculs de visibilité de Chazelle et Guibas [CG89] ou de Heffernan et Mitchell [HM90] par exemple).
Notre travail porte sur des scènes polygonales, c'est-à-dire des scènes composées de polygones simples ayant deux à deux une intersection nulle.

Fig. 1.1 -- Définition des polygones. a. Orientation
des sommets. b. Polygone avec trou.
Nous orientons les sommets d'un polygone de telle façon que le polygone soit localement à gauche de deux sommets consécutifs. Pour un sommet p nous notons p+ (resp. p-) le sommet suivant (resp. précédent) sur le polygone (figure 1.1a). Les polygones ont deux à deux une intersection nulle, mais un polygone peut en contenir un autre qui, s'il est correctement orienté, forme un trou (figure 1.1b). Ces trous peuvent à leur tour contenir d'autres polygones... Un polygone peut représenter un mur délimitant un bâtiment, mur dont les pans peuvent avoir des caractéristiques différentes (couleur, matière, réflectance, etc.). Ces pans devront être considérés individuellement lors de l'affichage de la scène par exemple. Il est alors plus facile de visualiser les polygones si nous avons directement la liste des côtés visibles à afficher plutôt que de la calculer à partir de la liste des polygones. Un côté de polygone peut aussi représenter une fenêtre, et nous voulons alors calculer la partie de la scène visible depuis ce côté seulement et non pas la partie visible depuis tout le polygone.
Par conséquent, les objets élémentaires que nous considérons dans les relations de visibilité ne sont pas les polygones eux-mêmes, mais les côtés de polygone. Pour nous, un polygone est un objet composite composé d'éléments ayant chacun leurs propriétés propres. De plus, ce point de vue permet de ne pas se préoccuper de la convexité ou non des polygones dans les algorithmes que nous étudions.
Les divers problèmes de visibilité étudiés peuvent être regroupés en deux catégories générales : calculs globaux et calculs locaux de visibilité.
Une grande catégorie de ces problèmes concerne les problèmes de gardiennage, appelés problèmes de galerie d'art en référence à la surveillance des oeuvres d'art dans les musées. L'énoncé type de ces problèmes est :
étant donné un polygone simple de n côtés, combien faut-il mettre de gardes aux sommets du polygone pour que tout point de la frontière intérieure du polygone soit visible d'au moins un garde, et comment placer ces gardes ?La réponse à cette question a été donnée par Chvátal [Ch85] qui a montré que E(n/3) gardes étaient toujours suffisants et parfois nécessaires. Avis et Toussaint [AT81] ont donné un algorithme de placement qui s'exécute en temps O(nlog n).
Divers variantes de ce problème ont été étudiées : spécialisation pour des polygones particuliers (en étoile, orthogonaux...), gardes mobiles le long d'une arête, surveiller l'extérieur du polygone, etc. Le livre d'O'Rourke [OR87] décrit en détails les divers problèmes de galerie d'art.
Des problèmes similaires se posent dans des calculs d'éclairage, où des sommets, des côtés de polygone, représentent des lampes illuminant l'intérieur du polygone.
Le calcul du graphe de visibilité, qui consiste à calculer toutes les paires de sommets de la scène mutuellement visibles, est un autre problème de calcul global de visibilité très étudié (il permet ensuite de faire des calculs de planification de trajectoire).
Les requêtes les plus courantes concernent le calcul des objets vus depuis un point de vue, que ce soit dans le contexte de calculs discrets comme dans le lancer de rayons ou dans le contexte de calculs continus comme dans le calcul d'une vue autour d'un point.
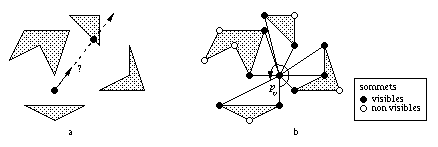
Fig 1.2 -- Requêtes locales de calcul de
visibilité. a. Calcul discret : lancer de
rayons. b. Calcul continu : calcul de vue.
L'énoncé d'une requête de lancer de rayons est :
soit un point et une direction de vision, quel est le premier objet de la scène intersecté par la demi-droite issue du point dans la direction donnée ? (figure 1.2a)Le lancer de rayons est utilisé en synthèse d'image pour visualiser une scène. L'image à calculer est déterminée par un point de vue et un écran de projection : c'est l'image de la scène obtenue sur l'écran quand elle est regardée à partir du point de vue. L'image est discrétisée en pixels (éléments de couleur uniforme) et pour la calculer, un rayon issu du point de vue et passant par le centre de chaque pixel est lancé dans la scène. La couleur résultante d'un pixel est celle du point de l'objet de la scène coupé par le rayon correspondant.
Ce calcul est discret : il ne concerne la visibilité que d'un rayon. Le calcul doit être refait à chaque fois que la direction de vision est modifiée, même si le point de vue reste le même.
La vue -- ou polygone de visibilité -- autour d'un point permet d'avoir une description continue dans l'espace objet de la visibilité autour du point de vue :
la vue autour d'un point pv est l'ensemble des sommets de polygone de la scène vus depuis ce point et classés par ordre angulaire. (figure 1.2b)
La vue code les limites de visibilité autour du point de vue : entre deux sommets consécutifs de la vue, l'objet vu depuis pv est le même. Cette description est une description continue de la visibilité depuis ce point : elle ne fait intervenir aucune discrétisation arbitraire.
Les calculs continus permettent parfois de résoudre plus efficacement des problèmes d'abord résolus par une série de calculs discrets. Par exemple, le calcul d'une image en lancer de rayons nécessite de lancer un rayon par tous les pixels de l'image alors que l'image résultante peut directement être obtenue par un calcul de vue : il suffit de déterminer la projection sur l'écran des limites de visibilité.
Nous venons de décrire des calculs statiques, où tous les objets concernés sont immobiles. Les calculs de visibilité ont aussi une grande importance dans des situations dynamiques, où les données du problème (objets de la scène, point de vue) varient au cours du temps.
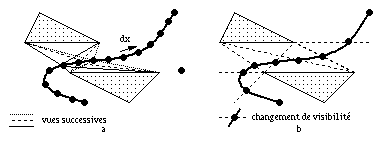
Fig. 1.3 -- Calcul de vue le long d'une trajectoire.
a. Calcul discret : recalcul à chaque
déplacement dx. b. Calcul
continu : calcul des limites de visibilité.
La simulation d'une personne en mouvement nécessite de pouvoir calculer la vue autour d'un point se déplaçant le long d'une trajectoire. Là aussi deux approches peuvent être envisagées pour ce calcul. Dans l'approche discrète, la vue est entièrement recalculée à chaque déplacement élémentaire dx du point de vue (figure 1.3a).
Cependant, pour accélérer les calculs il est préférable d'adopter une approche continue, c'est-à-dire de calculer les limites dans lesquelles l'ensemble d'objets vus reste le même et de faire, si possible, lors d'un changement de visibilité une mise à jour incrémentale moins chère qu'un recalcul complet (figure 1.3b).
L'utilisation de l'approche continue pour résoudre un problème de visibilité permet en général une résolution plus souple et plus économique. En effet, l'approche continue utilise la cohérence spatiale de la scène -- comme dans le cas du calcul d'une vue -- ou la cohérence temporelle du problème -- comme dans le cas du calcul d'une vue le long d'une trajectoire -- pour déterminer rapidement si la visibilité a changé et le cas échéant pour mettre à jour la visibilité sans devoir la recalculer entièrement. Les travaux que nous présentons dans cette thèse sont centrés sur l'utilisation de l'approche continue -- utilisation de la cohérence spatiale et temporelle -- pour répondre à des requêtes de calculs de visibilité statique et dynamique.
La cohérence spatiale ou temporelle ne peut cependant être pleinement utilisée que si certains calculs de visibilité ont déjà été effectués auparavant, notamment lors d'une phase de prétraitement.
Le prétraitement s'adresse aux calculs locaux de visibilité, cependant un calcul global de visibilité peut servir d'étape de prétraitement pour ces calculs locaux.
Nous nous intéressons dans cette thèse à la construction et à l'utilisation de structures globales pour accélérer les calculs de visibilité.