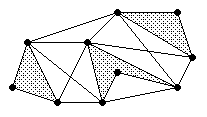
Fig. 1.10 -- Graphe de visibilité d'une scène.

Fig. 1.10 -- Graphe de visibilité d'une
scène.
Les arêtes du graphe de visibilité relient donc les sommets de la scène mutuellement visibles. La figure 1.10 montre la représentation géométrique du graphe de visibilité, où les segments correspondant aux arêtes du graphe ont été tracés dans la scène. Le graphe de visibilité contient au moins les arêtes correspondant aux côtés des polygones et aux segments de l'enveloppe convexe de la scène. Ce graphe n'est pas orienté, mais les arêtes incidentes à un sommet sont classées dans l'ordre dans lequel sont répartis les segments correspondants dans la scène.
Le nombre de sommets de ce graphe est le nombre total n de sommets des polygones. Son nombre d'arêtes, noté m, varie en revanche d'une taille linéaire (m=O(n)) à une taille quadratique (m=O(n2)). La taille minimale est obtenue quand chaque polygone ne voit qu'un seul polygone et qu'il n'y a que quatre arêtes de visibilité entre ces paires de polygones (figure 1.11a) ; la taille est alors m=n+4(np-1), où np est le nombre de polygones. La taille maximale est obtenue quand tous les sommets sont mutuellement visibles (figure 1.11b) ; le graphe de visibilité est alors le graphe complet Kn de taille maximale m=n(n-1)/2.
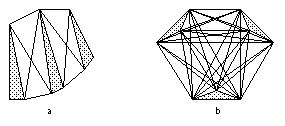
Fig. 1.11 -- Graphes de visibilité.
a. De taille minimale. b. De taille
maximale.
Les graphes de visibilité servent par exemple en planification de trajectoire : dans une scène de polygones, le plus court chemin évitant les obstacles entre deux points p et q emprunte les arêtes du graphe de visibilité (figure 1.12). Le calcul de ce chemin se ramène alors à un calcul de plus court chemin dans le graphe de visibilité, où le poids des arêtes du graphe est la longueur de l'arête géométrique (voir [LPW79]).
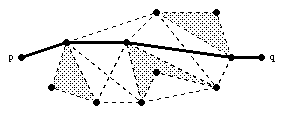
Fig. 1.12 -- Plus court chemin entre deux points en
présence d'obstacles.
L'algorithme naïf pour calculer le graphe de visibilité consiste à examiner toutes les paires (p,q) de sommets et à vérifier si les segments [p,q] correspondants ne sont pas coupés par un côté de polygone. Pour chaque paire, la vérification prend un temps O(n), soit un temps total de calcul en O(n3). Même si par chance il suffit de tester O(1) côtés pour les segments ne correspondant pas à une arête du graphe de visibilité, il faut tester les n côtés avant de s'apercevoir qu'un segment correspond à une arête de visibilité, soit un coût total de O(n2+(n-1)m). Que m soit linéaire ou quadratique, le temps de calcul est toujours n fois trop long par rapport au temps optimal O(n log n+m).
Grâce au balayage d'un espace de configuration annexe (un arrangement de droites), Edelsbrunner et Guibas [EG86] ont réduit le coût du calcul de graphe de visibilité d'une scène de n segments à un coût en O(n2), qui n'est optimal que pour le calcul de graphes denses. Overmars et Welzl [OW88] ont transposé ces techniques dans la scène de segments, ce qui leur a permis d'obtenir ensuite un algorithme sensible à la sortie, de complexité O(m log n). Ces algorithmes utilisent des notions et des techniques (dualité, balayage) au centre de nos travaux ; nous les détaillons dans les parties qui suivent, en les adaptant en général au cadre de scènes polygonales.
Entre-temps, Gosh et Mount [GM91] ont élaboré le premier algorithme de calcul de graphe de visibilité de polygones en temps optimal O(n log n+m). Ils utilisent un calcul incrémental (qui utilise donc un espace mémoire en O(m)) assez compliqué et reconnaissent eux-mêmes que leur algorithme est inutilisable en pratique, car les constantes impliquées dans le temps de calcul sont assez importantes. Nous ne détaillons pas cet algorithme dans ce mémoire.
Dans le cadre de scènes composées d'objets courbes convexes, Pocchiola et Vegter [PV96b] ont élaboré une nouvelle structure de données qui étend la notion de graphe de visibilité : le complexe de visibilité. Cette structure leur permet de calculer le graphe de tangence de la scène en temps optimal O(n log n+m), d'abord par un algorithme incrémental [PV96b], puis par un algorithme de balayage [PV96a].
En reprenant les concepts de complexe de visibilité, de dualité et de balayage dans le cadre de scènes polygonales, nous avons élaboré un nouvel algorithme de calcul de graphe de visibilité, le premier qui soit optimal en temps (O(n log n+m)) et en espace de travail (O(n)). Nous l'exposons en détail dans le chapitre suivant.
Nous exposons jusqu'à la fin de ce chapitre les techniques et les structures de données que nous utilisons ensuite dans nos travaux.
Il y a par exemple une correspondance naturelle entre les hyperplans et les points. La transformation la plus connue entre hyperplans et points est l'inversion de centre O, notée *, qui dans Rn associe à l'hyperplan H d'équation Sommei=1n ai xi+1=0 le point de coordonnées H* (a1,...,an). Cette bijection a la propriété d'inverser la relation d'inclusion : en notant H+ et H- les deux demi-espaces délimités par l'hyperplan H (H+ contenant O), alors pour tout point p
p E H (resp. H+, resp. H- <=> H*E p* (resp. p*+, resp. p*-).
Cette transformation permet alors de manipuler un ensemble de points, plus facile à manier que l'ensemble d'hyperplans de départ.
D'une manière générale, on appelle dualité toute bijection entre points et hyperplans qui inverse la relation d'inclusion. Nous détaillons maintenant l'utilité et l'utilisation de relation de dualité dans le cadre de problèmes de visibilité dans le plan.
Quand nous travaillons sur des problèmes de visibilité dans le plan, nous manipulons en fait des droites orientées qui représentent les directions de vision, et les objets vus sont ceux coupés par ces droites. Pour accélérer les calculs de visibilité, nous voulons classer les droites en différents ensembles qui les regroupent en fonction des objets qu'elles coupent. Ainsi, pour savoir par exemple quel objet est vu dans telle direction, il suffit d'identifier à quel ensemble appartient la droite correspondante et de consulter les propriétés de visibilité de cet ensemble, propriétés communes à toutes les droites de l'ensemble.
Il est difficile de manipuler directement des ensembles de droites : comment peut-on les représenter, tester l'appartenance d'une droite à un ensemble, ou définir les frontières communes entre ces ensembles ? L'utilisation de relations de dualité nous permet de transformer ces ensembles de droites en ensembles de points, plus faciles à appréhender.
Nous considérons l'espace des droites orientées. Ainsi, les deux droites passant par un point p et de vecteur directeur respectif v et -v, bien que géométriquement confondues, sont considérées comme étant deux droites distinctes.
Il y a plusieurs façons d'associer un point à une droite. Deux transformations souvent utilisées sont (figure 1.13a) :
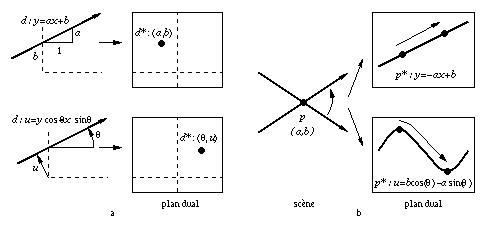
Fig. 1.13 -- Relations de dualité. a. Point
dual d'une droite. b. Courbe duale d'un point.
Ces deux relations ont beaucoup de propriétés communes, et leurs différences ne sont pas fondamentales (ce point est précisé plus loin). Dans la suite, la notation * désigne indifféremment l'une ou l'autre des deux relations quand les propriétés évoquées sont les mêmes ; s'il y a des différences, nous préciserons alors la relation concernée.
L'axe des abscisses du plan dual utilisé représente la pente (ou l'angle) des droites. Si d1 et d2 sont deux droites parallèles telles que d1 soit au-dessus de d2, alors les points duaux d1* et d2* ont même abscisse et d1* est au-dessus de d2*.
Pour résoudre les problèmes de visibilité que nous étudions, nous voulons, étant donné un côté de polygone (p,q), pouvoir considérer les droites qui coupent ce segment. Or une droite de direction theta coupe le segment (p,q) si et seulement si elle est située entre les droites de même direction theta et passant respectivement par p et q. Les droites passant par un sommet représentent des limites de visibilité, il est donc intéressant de considérer l'ensemble des droites passant par un sommet donné p=(a,b). À chaque droite passant par p est associé un point dans l'espace dual. Quand la droite tourne autour de p, le point dual décrit une courbe duale p* dans l'espace dual la droite d'équation y=-ax+b (dualité (a,b)) ou la sinusoïde d'équation u(theta)=b cos theta-a sin theta (dualité (theta,u)) (figure 1.13b).
Nous retrouvons avec ces courbes duales des propriétés d'inversion des relations d'inclusion. En effet, la courbe duale p* d'un point p représente dans le plan dual le graphe d'une fonction qui sépare le plan en deux demi-espaces p*+ (resp. p*-) est le demi-espace ouvert situé au-dessus (resp. en dessous) de la courbe p*. Nous avons alors les relations (figure 1.14a)
p E d (resp. d+, resp. d-) <=> d*E p* (resp. p*-, resp. p*+)}.
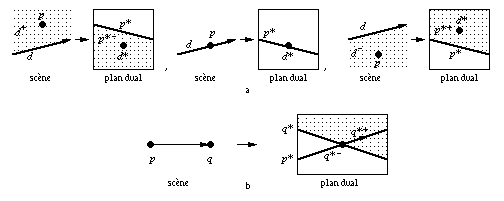
Fig. 1.14 -- Propriétés de la dualité.
a. Inversion de la relation d'inclusion.
b. Position relative et intersection dans le plan dual.
Ces courbes duales ont d'autres propriétés. Si nous considérons la droite orientée (p,q), alors dans l'espace dual les courbes duales p* et q* se coupent en le point dual (p,q)*, de telle façon que p* passe de q*- à q*+ (p* traverse q* de bas en haut) (figure 1.14b). Cette propriété permet d'obtenir directement dans l'espace dual des informations sur la position relative des objets par rapport à une direction de vision.
Reprenons notre côté de polygone (pq). Les deux courbes duales découpent l'espace dual en trois parties au-dessus, entre et en dessous des deux courbes. Alors une droite d coupe le segment (pq) si et seulement si son point dual d* est dans l'espace situé entre les deux courbes p* et q* (figure 1.15a). Si le point est au-dessus (resp. en dessous) de cette région, alors le segment est en dessous (resp. au-dessus) de la droite. Cette partition de l'espace dual correspond à une partition de l'ensemble des droites en fonction de leur position relative par rapport au segment.
Considérons maintenant une scène composée de polygones. Nous appliquons le découpage de l'espace dual précédent pour chaque côté de polygone. Nous obtenons alors un découpage de l'espace dual par les courbes duales des sommets des polygones l'arrangement dual de la scène (figure 1.15b).
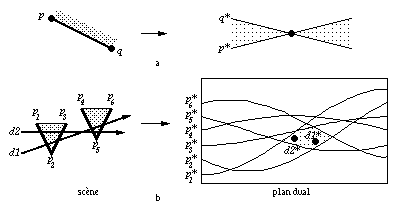
Fig. 1.15 -- Classification des droites grâce à la
dualité. a. Zone d'un côté de
polygone. b. Arrangement dual de la scène
droites correspondant à une face.
Cet arrangement dual est composé de faces, d'arêtes (portions de courbes comprises entre deux sommets) et de sommets (intersection de deux courbes). Les faces représentent les ensembles de droites intersectant une même liste d'objets (dans l'ordre de la liste).
Plus précisément, à chaque droite d nous associons une étiquette, constituée des objets intersectés dans l'ordre par la droite. Si la droite coupe le segment ouvert Oi, alors nous mettons Oi dans l'étiquette. Si la droite passe par un sommet p, alors nous mettons p±± dans l'étiquette le premier signe de p±± est + (resp. -) si le côté (p-,p) du polygone est au-dessus (resp. en dessous) de la droite ; le deuxième signe de p±± est + (resp. -) si le côté (p,p+) du polygone est au-dessus (resp. en dessous) de la droite. La relation
d ~d' si et seulement si d et d' ont la même étiquette et on peut déplacer continûment d vers d' en gardant l'étiquette constante,est une relation d'équivalence. Les éléments de l'arrangement dual représentent les classes d'équivalence de cette relation.
Les deux relations de dualité évoquées jusqu'à maintenant sont très liées. Nous avons vu un certain nombre de propriétés communes, et elles sont liées de plus par la correspondance a= tan theta et b=u cos theta. Cependant la dualité (a,b) paraît plus limitée elle ne permet de ne considérer que les droites orientées de direction comprise dans l'intervalle ]-pi/2,pi /2[. Mais ces limitations ne sont pas importantes ici, car nous ne nous servons que des informations topologiques de l'arrangement dual, et les tests numériques sont tous retranposés sur les points et les droites de la scène.
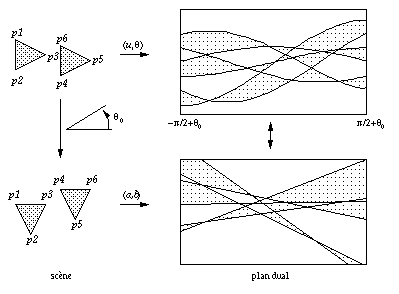
Fig 1.16 -- Correspondance entre les deux relations de dualité.
De plus, la partie de l'arrangement dual de courbes (dualité (theta,u)) compris dans l'intervalle ]theta0-pi/2,theta0+pi/2[ d'une scène et l'arrangement dual de droites (dualité (a,b)) de la scène à laquelle une rotation d'angle theta0 a été appliquée sont topologiquement identiques (figure 1.16, où nous avons colorié des faces pour mieux faire apparaître les correspondances). Enfin, pour avoir toutes les informations de visibilité, il suffit de se restreindre à un intervalle de directions de longueur pi, car les droites de direction theta et theta+pi sont géométriquement identiques. Cela se traduit par des relations de symétrie dans l'arrangement dual de courbes (dualité (theta ,u)). Pour visualiser un intervalle de directions de longueur 2pi avec les arrangements de droites, il suffit de « coller » à l'arrangement son symétrique par rapport à l'axe des abscisses.
Nous utilisons ici dans nos représentations de l'espace dual la formulation (a,b), car elle est plus pratique pour nos illustrations. Cependant nous ne nous servons que des informations topologiques, et non pas géométriques, des droites duales. Nous n'excluons donc aucune droite (verticale) dans l'espace dual.
La formulation (theta,u) est plus pratique à utiliser dans le cadre de scènes composées d'objets courbes, où les courbes duales correspondent aux droites tangentes aux objets. Pocchiola [Poc90] utilise cette dualité pour construire l'arrangement dual d'une scène d'objets convexes courbes.
Pour savoir quels sont les objets traversés par une droite, il suffit de localiser l'élément de l'arrangement qui contient le point dual. Il existe deux tactiques pour construire cet arrangement de droites : construction incrémentale et balayage.
La construction incrémentale consiste à introduire les droites une par une. Supposons que nous avons déjà construit l'arrangement de n-1 droites. Nous introduisons la ne droite, en cherchant les faces de l'arrangement traversées par cette droite, faces qui seront coupées en deux. Pour cela, il faut d'abord chercher la face semi-infinie gauche où commence cette droite. Ensuite, pour trouver le point de sortie de la face courante traversée, il suffit de parcourir les arêtes bordant la face -- dans le sens trigonométrique direct par exemple -- depuis l'arête d'entrée (figure 1.17).
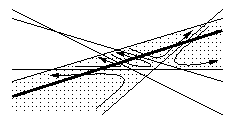
Fig 1.17 -- Construction incrémentale d'un arrangement
faces traversées par la nouvelle droite insérée.
Le théorème de la zone ([EOS86], [CGL85]) indique que le nombre total d'arêtes bordant les faces traversées par la droite est linéaire en fonction du nombre de droites de l'arrangement. La construction incrémentale d'un arrangement de n droites s'effectue donc en temps optimal O(n2).
Le balayage de l'arrangement consiste à parcourir les éléments de l'arrangement comme s'ils étaient balayés de la gauche vers la droite par une ligne. Le balayage est modélisé par la liste (eik)1<=k<=n{ des arêtes « coupées » par la ligne de balayage, où il y a pour chaque sommet de la scène exactement une arête portée par la courbe duale de ce point (figure 1.18a).
Le processus de balayage est en fait discret le balayage progresse en passant à chaque fois un sommet incident à deux arêtes consécutives eik et eik+1 de la coupe. La coupe est alors mise à jour en remplaçant ces deux arêtes par les arêtes suivantes e'ik et e'ik+1 respectivement sur les droites support de ik+1 et ik (figure 1.18b).
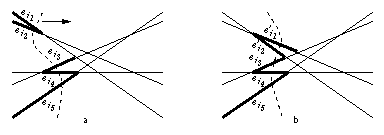
Fig. 1.18 -- Balayage d'un arrangement de droites. a. Coupe
de balayage. b. Progression du balayage.
La façon la plus directe d'effectuer ce balayage est de parcourir les sommets de l'arrangement dans l'ordre selon les abscisses croissantes. Cela revient à prendre une ligne de balayage verticale « droite ». Le balayage nécessite alors l'utilisation d'une queue de priorité et s'effectue en temps O(n2log n). Cependant ce type de balayage\ est trop strict et un balayage topologique plus souple suffit. Le balayage topologique parcourt les sommets de façon cohérente il ne passe un sommet v=di ^ dj qu'après avoir déjà visité les sommets précédents sur di et dj.
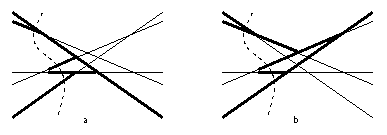
Fig. 1.19 -- Arbres d'horizon. a. Arbre
supérieur. b. Arbre inférieur.
Pour effectuer ce balayage, Edelsbrunner et Guibas [EG86] ont créé une structure de données auxiliaire : les arbres d'horizon. Étant donné une coupe de balayage, l'arbre d'horizon supérieur (resp. inférieur) est construit en étendant chaque arête de la coupe vers la droite jusqu'à ce qu'elle rencontre une droite de l'arrangement de pente plus petite (figure 1.19) (remarque : Edelsbrunner et Guibas [EG86] utilisent la dualité d : y=ax+b -> d* (a,b), qui inverse certaines relations par rapport à la dualité que nous utilisons. Nous avons retransposé ici la description de l'algorithme avec la dualité que nous utilisons). Alors le balayage peut progresser en passant un sommet v si et seulement si v est présent dans les deux arbres d'horizon v est alors intersection de deux arêtes consécutives de la coupe.
Pour mettre à jour l'arbre d'horizon supérieur après le passage d'un sommet v=eik ^ eik+1, il faut trouver la nouvelle extrémité droite du segment porté par la droite ik+1. Pour cela, il suffit de parcourir les arêtes de la baie formée par les arêtes successives de l'arbre d'horizon et commençant par l'arête eik-1 de la coupe située juste au-dessus (figure 1.20).
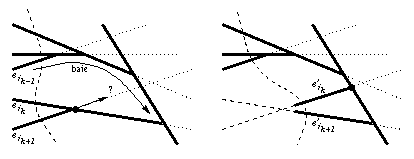
Fig. 1.20 -- Mise à jour de l'arbre d'horizon lors du passage d'un
sommet.
La mise à jour à chaque passage coûte a priori un temps O(n), car une baie peut comporter O(n) arêtes, soit pour les O(n2) passages un temps total O(n3). Cependant, grâce à un schéma de comptage global, les auteurs montrent dans [EG89] qu'au total seulement O(n2) arêtes sont balayées dans les baies. Le balayage topologique s'effectue alors en temps optimal O(n2).
Nous avons présenté cet arrangement dual comme permettant de résoudre des problèmes liés à la visibilité. Il permet en effet de calculer le graphe de visibilité de la scène, comme nous allons le voir ci-après, et de faire des calculs de vues, comme nous le verrons dans le chapitre 3.
Cependant cet arrangement de droites permet de résoudre d'autres problèmes géométriques, comme calculer le triangle d'aire minimale formé par 3 points parmi n points donnés, calculer une droite coupant le plus possible de segments parmi n segments donnés, tester la dégénérescence de d+1 points dans Rd, etc. (voir par exemple [EG89] et [CGL85] pour d'autres applications).
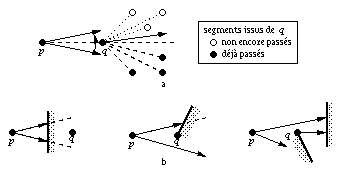
Fig. 1.21 -- Balayage de l'arrangement. a. Cohérence
du balayage. b. Mise à jour de l'objet vu lors du
passage d'un segment (p,q).
À chaque sommet p de la scène est alors associé l'objet vu depuis p par tout rayon appartenant dans l'espace dual à l'arête e de la coupe associée à p. Lors du passage du sommet v correspondant au segment (p,q), la mise à jour de l'objet vu depuis p connaissant celui vu depuis q se fait alors en temps constant (la figure 1.21(b) montre les situations à considérer) et vérifier si (p,q) est une arête du graphe de visibilité est immédiat.
Overmars et Welzl [OW88] ont remarqué qu'un seul arbre d'horizon pouvait suffire pour effectuer le balayage il suffit alors de toujours passer le sommet en bas à gauche de l'arbre d'horizon supérieur, sommet qui peut être mis à jour en temps constant à chaque passage. Ils ont alors transposé les arbres d'horizon de l'espace dual dans la scène, où ils deviennent des arbres de rotation} comme déplacer un point sur une droite d dans le plan dual revient à faire tourner dans la scène une droite passant par le point d*, balayer l'arrangement de droites dual revient à faire un balayage rotationnel dans la scène, c'est-à-dire à faire pivoter des droites autour des sommets de la scène.
Overmars et Welzl innovent ensuite pour tenir compte directement des relations de visibilité au lieu d'étendre une demi-droite, ils étendent un demi-rayon libre maximal, qui s'arrête donc sur le premier objet rencontré.
L'arbre de rotation est alors défini pour une direction theta à chaque sommet p de la scène, est associé le premier sommet vu depuis p en tournant dans le sens trigonométrique direct depuis la direction theta (figure 1.22). Un point fictif d'abscisse plus grande que celles des points de la scène et d'ordonnée infinie est ajouté à la scène en tant que sommet susceptible d'être vu.
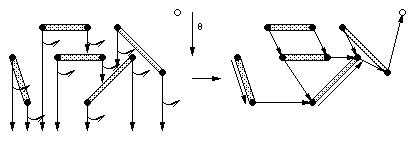
Fig. 1.22 -- Arbre de rotation d'une scène de segments.
Ce graphe est un sous-graphe de taille n du graphe de visibilité. Le maintien de cet arbre quand theta varie de -pi/2 à pi/2 permet de trouver toutes les arêtes du graphe de visibilité. Le maintien se fait, comme pour les arbres d'horizon, de façon discrète l'arête de plus petite pente est passée à chaque fois, ce qui assure en plus la cohérence du balayage.
L'étude des propriétés géométriques du graphe induites par le balayage droit conduit les auteurs à considérer des chaînes d'arêtes, suites maximales d'arêtes consécutives telles que les segments de la scène incidents aux sommets d'une chaînes soient au-dessus de la chaîne.
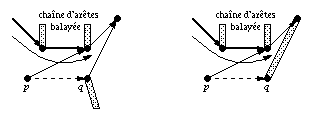
Fig. 1.23 -- Mise à jour de l'arbre de rotation lors du passage d'une
arête.
Lors du passage de l'arête (p,q), la nouvelle extrémité r de l'arête issue de p est le point de tangence des droites passant par p et d'une chaîne d'arêtes déterminée (figure 1.23). Ce point est trouvé en balayant les arêtes de la chaîne.
L'utilisation de la queue de priorité coûte un temps O(m log n). Le coût du balayage des arêtes lors des mises à jour pourrait être dans le pire cas O(mn). Les auteurs annoncent (sans preuve détaillée) que le coût total n'est que de O(alpha(n) m). En fait le chapitre suivant montre implicitement que cette complexité de balayage n'est au total qu'en O(m).
Une première version du complexe de visibilité a été donnée par Vegter [Veg90] pour des scènes de segments, sous le nom de diagramme de visibilité. Le complexe est ensuite pleinement étudié par Pocchiola et Vegter [PV96b] dans le cadre de scènes d'objets courbes convexes. Nous présentons ici (de manière moins formelle et moins combinatoire) le complexe de visibilité dans le cadre de scènes polygonales.
Le complexe de visibilité comporte trois sortes d'éléments des faces, des arêtes et des sommets.
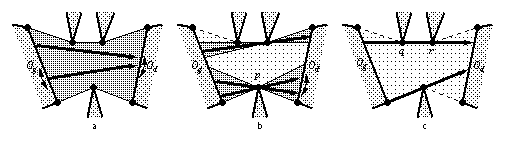
Fig. 1.24 -- Éléments du complexe de
visibilité. a. Face. b.
Arêtes. c. Sommets.
Les faces sont des éléments de dimension deux elles représentent les rayons d'étiquette (Og,Od), c'est-à-dire les rayons qui partent de Og et arrivent à Od sans toucher d'autre objet. Un tel rayon a donc deux degrés de liberté (figure 1.24a).
Les arêtes sont des éléments de dimension un elle représentent les rayons d'étiquette (Og,p±±,Od), c'est-à-dire les rayons allant de Og à Od en passant par un sommet p. Ces rayons n'ont plus qu'un seul degré de liberté ils doivent passer par p (figure 1.24b).
Les sommets sont des éléments de dimension zéro ils représentent les rayons d'étiquette (Og,q±±,r±±,Od), c'est-à-dire le rayon allant de Og à Od en passant par q et r. Ces rayons sont fixés ils doivent passer par deux sommets (figure 1.24c).
De la même façon qu'il était plus facile de représenter les classes de droites dans l'espace dual grâce à l'arrangement de droites dual, nous représentons aussi les éléments du complexe de visibilité en utilisant cet espace dual. En effet, un segment libre maximal est inclus dans une droite support; nous représentons alors un tel segment par le point dual de sa droite support. L'espace dual nous permet de mieux visualiser les relations entre les divers éléments du complexe (figure 1.25).
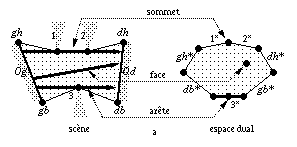
Fig. 1.25 -- Éléments du complexe de
visibilité visualisation dans l'espace dual.
Un sommet représente un rayon passant par deux sommets p et q. Dans l'espace dual c'est donc un point, intersection des deux courbes duales p* et q* associées aux deux sommets. Une arête représente des rayons de visibilité constante passant par un sommet p, qui sera dit sommet associé à l'arête. Dans l'espace dual, une arête est donc une portion de la courbe duale p* associée au sommet, délimitée par deux sommets du complexe. Une arête est incidente à deux sommets, appelés respectivement sommet gauche et sommet droit (figure 1.26a). Un sommet est incident à quatre arêtes, appelées arêtes gauche/droite-haute/basse (figure 1.26b).
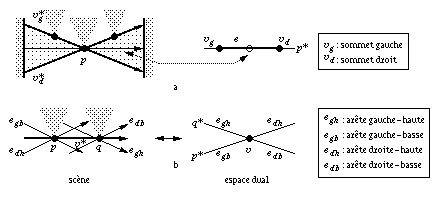
Fig. 1.26 -- Relations d'incidences entre a.
arête et sommets, b. sommet et arêtes, dans
le complexe de visibilité.
Les arêtes sont classées en six catégories, en fonction de la géométrie locale du polygone autour du sommet p associé (figure 1.27) arête l-convexe, l-concave, m-convexe, m-concave, n-gauche et n-droit. Selon sa catégorie, une arête peut être incidente à une, deux ou trois faces. D'une manière générale, nous désignons quatre faces incidentes à une arête par face gauche/droite-haute/basse, même si certaines de ces faces sont nulles ou confondues.
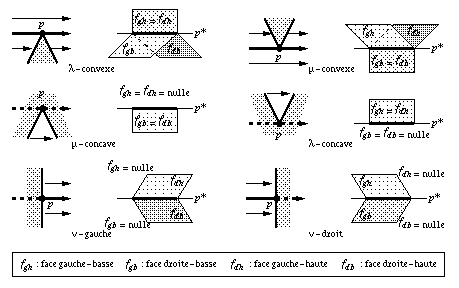
Fig. 1.27 -- Les différents types d'arêtes du complexe.
Considérons maintenant une face du complexe, associée à (Og,Od). Nous voyons qu'il existe un seul rayon de pente minimale (resp. maximale) dans cette face. Ces deux rayons correspondent à deux sommets extrêmes bordant la face, dits sommets gauche et droit de la face. Si nous prenons maintenant un rayon appartenant à cette face, alors nous pouvons le translater vers le bas (resp. vers le haut) en gardant la même visibilité, jusqu'à ce que nous rencontrions un sommet qui provoque, si nous continuons le déplacement, un changement de visibilité. Les deux rayons extrêmes appartiennent chacun à une arête bordant la face. En fait, la face est bordée par deux chaînes d'arêtes, une chaîne supérieure et une chaîne inférieure, toutes deux délimitées par les deux sommets extrêmes de la face. La face délimite dans la scène une région géométrique, limitée par les segments de droite associés aux sommets des chaînes d'arêtes (sommets extrêmes exclus). La figure 1.28 montre les éléments du complexe qui délimitent une face.
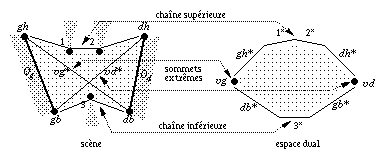
Fig. 1.28 -- Éléments délimitant une face du complexe.
Si nous traçons la face dans l'espace dual en utilisant la dualité (a,b), nous voyons que c'est un polygone convexe. Cette caractéristique est due à une propriété plus générale des faces si nous prenons dans l'espace dual deux points dans une face, alors la courbe duale passant par ces deux points est, entre ces deux points, entièrement contenue dans la face. Cela signifie dans la scène que si nous prenons deux rayons r1 et r2 dans la face et notons p=r1 ^ r2 le point d'intersection des deux droites support des rayons, alors si nous déplaçons r1 vers r2 en faisant pivoter sa droite support autour de p, alors il ne quitte pas la face. En effet, les deux frontières de la face (les chaînes d'arêtes) sont convexes par visibilité. Cela signifie notamment que dans la scène, chaque sommet du bord haut de la face est visible des sommets du bord bas de la face et réciproquement.
Les arêtes peuvent encore être classées en deux catégories. En effet, une arête bordant une face (Og,Od) peut soit avoir aussi la visibilité (Og,Od), soit passer par l'une des extrémités de Og ou Od. Dans ce dernier cas, la face peut être bordée par une série d'arêtes consécutives portées par la même courbe duale (figure 1.29).
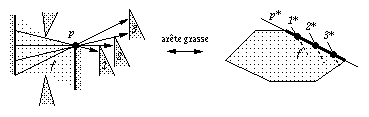
Fig. 1.29 -- Arêtes grasses.
De telles arêtes sont dites grasses (terminologie empruntée à Pocchiola et Vegter [PV96b], car une portion de courbe duale est décomposée en sous-arêtes bordant une même face. Chacune des deux chaînes d'arêtes d'une face peut avoir deux séries d'arêtes grasses une en début de chaîne (arête grasse gauche) et une en fin de chaîne (arête grasse droite).
Contrairement à l'arrangement de courbes dual, le complexe de visibilité n'a pas une structure plane. En effet, des segments libres maximaux différents peuvent être contenus dans une même droite support. Ils sont représentés alors dans le plan dual par un même point dual. Nous plongeons ce plan dans R3, où ces points duaux sont « décollés » (figure 1.30).
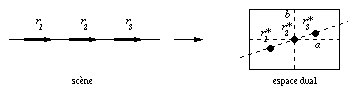
Fig. 1.30 -- Utilisation d'une dimension supplémentaire pour
représenter les rayons confondus en projection dans le plan dual.
La figure 1.31 montre la structure non plane du complexe au voisinage de l'un de ses sommets et montre les deux situations dans la scène correspondant à la coupe du complexe avant (resp. après) le sommet. En particulier, deux courbes duales qui se coupent en projection dans le plan dual ne se coupent pas forcément en un sommet dans le complexe, comme c'était le cas dans l'arrangement dual elles se coupent seulement si les deux points associés sont mutuellement visibles.
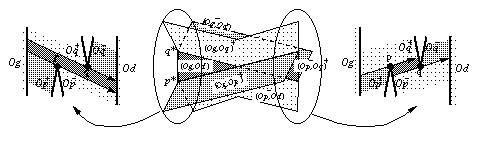
Fig. 1.31 -- Non planarité du complexe au voisinage d'un sommet.
La configuration du complexe autour d'un sommet (nombre de faces incidentes, relations d'incidence) correspondant à l'arête de visibilité [p,q] dépend alors de la configuration géométrique de la scène autour des points p et q. La figure 1.32 montre les 17 configurations géométriques possibles autour de ces sommets.
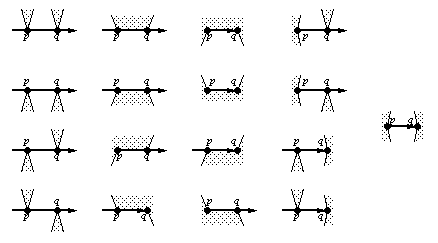
Fig. 1.32 -- Différentes configuration géométriques
correspondant à un sommet du complexe.
Il définit d'abord pour chaque segment s une subdivision Vis(s,S) (S désigne la scène) qui représente la classification en classe d'équivalences des rayons issus de s. Vis(s,S) est donc l'ensemble des faces du complexe de visibilité qui ont dans leur étiquette pour objet gauche le segment s. Ces faces sont donc comprises dans l'espace dual entre les deux courbes duales p1* et p2* des deux extrémités p1 et p2 du segment s (figure 1.33a). Parmi les sommets de Vis(s,S), ceux situés sur p1* (resp. p2*) ne sont incidents qu'à trois arêtes. Les arêtes ne sont incidentes qu'à la face (resp. qu'aux deux faces) qu'elles bordent dans Vis(s,S). Le diagramme de visibilité est alors constitué de l'ensemble de ces subdivisions Vis(s,S). Ces subdivisions sont reliées entre elles grâce aux arêtes partenaires. Un rayon issu du segment s et passant par le sommet p d'un segment s' avant d'être arrêté par un segment O peut-être associé soit à l'arête e bordant les faces f(s,s') et f(s,O) de Vis(s,S), soit à l'arête e' bordant la face f(s',O) de Vis(s',S) (figure 1.33b). Les deux arêtes e et e' sont alors dites partenaires et ont chacune un pointeur sur l'autre.
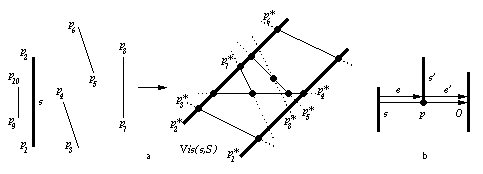
Fig. 1.33 -- Diagramme de visibilité. a.
Décomposition Vis(s,S) du diagramme de
visibilité. b. Arêtes partenaires
e et e'.
Les calculs sont plutôt considérés dans une subdivision Vis(s,S), avec occasionnellement un passage d'une subdivision à une autre par l'intermédiaire d'arêtes partenaires. Le diagramme de visibilité et le complexe de visibilité sont équivalents. La représentation du complexe que nous utilisons, adaptée de celle de Pocchiola et Vegter [PV96b],est un peu plus uniforme.
Nous montrons dans le chapitre suivant comment calculer de façon optimale le complexe de visibilité d'une scène polygonale.