- L'application
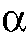est une involution sans point fixe.
- L'application
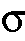est une permutation de B.
- L'application
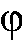est une permutation de B.
La recherche en modélisation 3D est née avec la Conception
Assistée par Ordinateur (CAO).
Elle a évolué depuis 1988 en intégrant la combinatoire et la
topologie à la géometrie et à l'algorithmique.
Des modèles issus de la notion de carte ont été
proposés à Strasbourg [Li88], à Besancon [AK89] et à
Mulhouse [Sp90].
Le thème de recherche de
Yves Palma
(à l'on doit cette page) porte sur ce dernier modèle appelé
pavage.
Un pavage est composé de 4 éléments :
est une involution sans point fixe.
est une permutation de B.
est une permutation de B.
L'idée (intuitive) de base de cette modélisation est d'associer chaque
partie de l'espace à un pavé (composé de brins).
Chaque pavé peut être comparé à une pièce d'un puzzle
dont l'image finale serait l'espace de dimension 3.
Un pavé dans la notion de pavage est une carte combinatoire, c'est-a-dire un ensemble de
brins reliés entre eux par
et .
Un pavage est un ensemble de cartes combinatoires reliées entre elles par
.
Un pavage est donc noté P=(B,
,
,
).
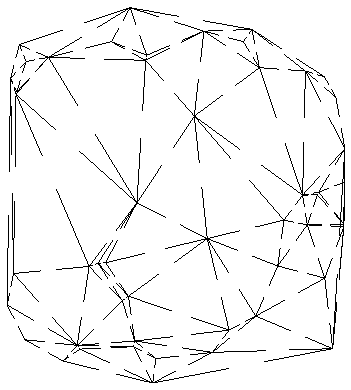
La carte (dans le plan 2D) comme le pavage (en 3D+) permet de représenter les diagrammes de Delaunay et de Voronoï.
,
) où B est un ensemble fini,
est une involution sans point fixe et
une permutation de B est appelé une carte.
Tout élément de B est appelé un brin.
de permutations
de B, <> est le groupe de
permutations de B engendré par ,
pour tout b de B, <>(b)={o(b); o
<>} est l'orbite de b
relativement au groupe <>.
(b) sont dits opposés.
>(b) = {b,
(b)} est appelé l'arête
de b dans C.
>(b) = {b,
(b), ...} est appelé le
sommet de b dans C.
-1
o >(b) est appelé la face
directe de b.
Pour toutes questions contactez moi.